计数知识

Author

2024-02-09 4337 words 9 minutes

Contents

这是本科时候的一些笔记内容，稍微整理了一下。

Falling and Rising Factorial

中文：降次幂 / 升次幂

升/降幂可以构成一组多项式基，任何以表示的多项式都可以改写成的形式，反之亦然。

Generalized Binomial Coefficients

当是整数时，退回到普通的组合数定义。当时，因为 0 因子，，也是符合直觉的定义。

二项式定理

扩展版本的二项式定理（也叫牛顿级数）

把二项式定理的指数扩展到实数

推论

利用二项式定理，带入次单位根（），可以求每隔个的二项式系数求和。例如

多项式定理

把二项式定理的变量推广到多个。设是正整数。对于所有的，有

把用分配律将这个乘积完全展开，用这种方法得到的结果共有项，而且每一项都可以写成的形式，其中是非负整数，其和为。合并同类项后，考虑每个前面的系数。通过选择个因子中的个为，剩下的个因子中的个为，，这样一直做下去直到令剩下的个为，最终得到项。根据乘法原理，项前面的系数等于

Generating Function

Some Examples

一些数列对应的生成函数

用生成函数计数

在所有由组成的位数中，的个数为偶数的有多少？设个数为，按照的个数讨论，知设，则

因此。

在所有由 1，2，3 组成的位数中，满足 1 的个数为偶数，2 的个数为奇数的有多少？

设满足条件的位数的个数为，记。注意到，由 1，2，3 组成的位数共有个。另外，。由此可知，当不做限制时，数字1，2，3各自对的生成函数“贡献”了一个因子。现在要求 1 的个数为偶数，那么 1 贡献的因子变为

要求 2 的个数为奇数，那么 2 贡献的因子变为对 3 不做要求，则它贡献的因子仍为。综上，的生成函数为因此，，则。

在所有由 1，2，3 组成的位数中，满足 1 的个数为偶数，2 的个数被 3 整除的有多少？设满足条件的位数的个数为，记，为的生成函数。由于 1 的个数为偶数，则对应的因子为由于 2 的个数为 3 的倍数，则中对应的因子为其中为 3 次单位根。由于对 3 不做要求，则中对应的因子为。综上（令），因此，。

Fibonacci Sequence

略

Catalan Number

考虑三柱汉诺塔问题的一个变种。现在有从左到右编号为 1、2 和 3 的 3 根柱子，初始状态 1 号柱子套着个圆盘，从上到下编号依次为，其他两根柱子均为空。现在需要把所有圆盘通过若干步移动转移到 3 号柱子上。对于每步移动，有如下限制：

1 号柱的盘子只能转移到 2 号柱上，2 号柱的盘子只能转移到 3 号柱上；
只允许移动某根柱子最上面的盘子。那么，不同的转移方案共能得到多少种编号的排列（按照从上到下的顺序）？

记移动个圆盘能得到的排列数为。根据移动规则，1 号圆盘首先进入 2 号柱。在这之后，1 号圆盘既有可能直接离开 2 号柱，也有可能停留在 2 号柱上。这提示我们可以根据 1号圆盘何时离开 2 号柱对可行方案进行分类（把 2 号柱看做一个栈，这相当于根据这个栈首次清空的时间进行分类）。若 1 号圆盘是第个离开 2 号柱的圆盘，则有个圆盘已经到达了 3 号柱，产生的排列数为，还有个圆盘在 1 号圆盘之后到达 3 号柱，产生的排列数为。根据加法原理和乘法原理，它的前几个初值为，。

令，求解可得，考虑到，故舍去。因此有，上式使用了公式，，这是因为

综上，。

接下来我们介绍若干出现卡塔兰数的例子。

矩阵分组相乘

作为例子，考虑三个矩阵，，相乘的问题。若按顺序相乘，前两个矩阵相乘需要次乘法，得到一个的矩阵；它再与第三个矩阵相乘，仍需要次乘法。为了得到最终结果，共进行了次乘法运算。若先让后两个矩阵相乘（需要进行m次乘法运算），再与第一个矩阵相乘（需要进行m次乘法运算），则总共进行了次乘法运算。由此可见，不同的相乘顺序（方案）的运算时间不同。最优的乘法顺序可以通过动态规划求得。这里我们不考虑如何寻找最优的方案，转而考虑矩阵相乘的方案数。

对个矩阵，共有多少种不同的方案计算？

记个矩阵相乘的方案数为。易知，，。观察到，个矩阵相乘时，每种方案恰好对应于一棵二叉树。以为例，五种相乘方案对应于如下五棵二叉树：

graph TD;

%% b4, b5, b6, b7 as leaves
subgraph b
b1(( )) --- b2(( ))
b1(( )) --- b3(( ))
b2(( )) --- b4(( ))
b2(( )) --- b5(( ))
b3(( )) --- b6(( ))
b3(( )) --- b7(( ))
style b4 fill:#66ccff
style b5 fill:#66ccff
style b6 fill:#66ccff
style b7 fill:#66ccff
end

%% a3, a5, a6, a7 as leaves
subgraph a
a1(( )) --- a2(( )) 
a1(( )) --- a3(( ))
a2(( )) --- a4(( ))
a2(( )) --- a5(( ))
a4(( )) --- a6(( ))
a4(( )) --- a7(( ))
style a3 fill:#66ccff
style a5 fill:#66ccff
style a6 fill:#66ccff
style a7 fill:#66ccff
end

graph TD;

%% d2, d4, d6, d7 as leaves
subgraph d
d1(( )) --- d2(( )) 
d1(( )) --- d3(( ))
d3(( )) --- d4(( ))
d3(( )) --- d5(( ))
d5(( )) --- d6(( ))
d5(( )) --- d7(( ))
style d2 fill:#66ccff
style d4 fill:#66ccff
style d6 fill:#66ccff
style d7 fill:#66ccff
end

%% c3, c4, c6, c7 as leaves
subgraph c
c1(( )) --- c2(( )) 
c1(( )) --- c3(( ))
c2(( )) --- c4(( ))
c2(( )) --- c5(( ))
c5(( )) --- c6(( ))
c5(( )) --- c7(( ))
style c3 fill:#66ccff
style c4 fill:#66ccff
style c6 fill:#66ccff
style c7 fill:#66ccff
end

graph TD;

%% e2, e5, e6, e7 as leaves
subgraph e
e1(( )) --- e2(( ))
e1(( )) --- e3(( ))
e3(( )) --- e4(( ))
e3(( )) --- e5(( ))
e4(( )) --- e6(( ))
e4(( )) --- e7(( ))
style e2 fill:#66ccff
style e5 fill:#66ccff
style e6 fill:#66ccff
style e7 fill:#66ccff
end

例如，图 a 表示的相乘方案为，图 b 表示的相乘方案为，以此类推。上图的二叉树，每一棵都有个结点，其中个叶子结点，个中间结点，且中间结点都有两个孩子。每个结点都代表一个矩阵。其中个叶子结点分别代表。中间结点代表的矩阵由它的左孩子代表的矩阵乘以右孩子代表的矩阵得到。因此根节点代表的矩阵就是。现在，求矩阵相乘的方案数的问题转化为了求上述二叉树的个数的问题。

现在对二叉树进行编码。把向左的边标记为1，向右的边标记为0。给定一棵二叉树，对其使用先序遍历。每当遇到一条未曾经过的边时，记录下它的标记。则遍历结束后，得到一个长度为的 01 串。以为例，图 a 可以表示为 111000，图 b 为 110010，图 c 为110100，图 d 为 101010，图 e 为 101100。继续观察可发现，若有片叶子，则 01 串中有个 1 和个 0，且 01 串前（）个数中，1 的个数不少于 0 的个数。由于二叉树和01串编码是一一对应的，因此求解矩阵相乘的方案数等价于求如下问题：

在由个 1 和个 0 组成的长为的所有序列中，满足其任意前缀中 1 的个数不少于 0 的个数的有多少？

这与之前的汉诺塔问题变种类似。盘子必须先进栈（对应于 1），而后再出栈（对应于 0），且在任意时刻，进栈的次数不少于出栈的次数。因此答案为第项卡特兰数，而例1的答案为。

排队进公园

有个人，个人有 10 元面额的现金，个人有 5 元面额的现金，售票员处没有零钱，公园的门票是 5 元。这个人排队进入公园，一旦售票处找不开零钱，则售票系统瘫痪。问有多少种不同的排队顺序，使得这个人都能够顺利进入公园？

括号匹配计数

对括号共能组成多少种合法的括号序列？

带限制的格点路径计数

这是另一个推导出卡塔兰数的途径，无需借助生成函数，而只需要一些组合技巧。

一个质点需要从处沿整点走到处，每次只能移动单位距离。那么在所有路径中，质点始终位于直线下方（包括）的有多少条?

若没有任何限制，路线需要走步，其中步向右，步向上，因此有条路径。现在要求质点始终位于下方。反过来，我们计算穿过直线的路径的数目。考虑某条穿过直线的路径。设它在上的点处第一次穿过。由于质点在整点上移动，这条路径此时到达了上的点。记路径中从到的部分为，从到的部分为。令表示由关于直线做对称得到的路径。则为由到的路径。那么为由到的路径。因此，一条穿过且由到的路径，对应于一条穿过且由到的路径。对于后者，由于由到的路径一定会穿过，因此“穿过 ”这一限制是多余的。那么，路径（或等价地，路径）的个数为。因此，从到且始终在下方的路径的个数为。

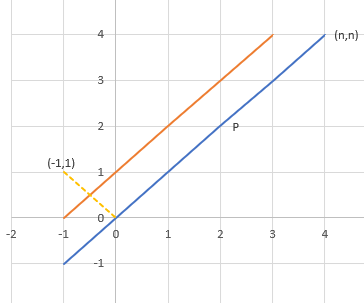
1-3-2-Avoid 排列

一个排列是 1-3-2-avoid，当且仅当对任意满足的三个数，它们在排列中的相对顺序不能是在的前面且在的前面。在的所有排列中，共有多少个满足 1-3-2-avoid？记满足1-3-2-avoid的排列数为。易知，，，，。一般地，若数字放置在排列的第个位置上，为了满足题目条件，排列的前个位置上的任意一个数字都必须大于排列的后个位置上的任意一个数字。由此可知，左侧的个位置上放置的是数字；右侧的个位置上放置的数字是。这两组数各自需要满足1-3-2-avoid性质，根据乘法原理，共有种可能。再根据加法原理，有由初始条件和递归关系可知，，为卡特兰数。

Stirling Number

斯特林数描述了普通多项式基，降幂基和升幂基之间的转换关系。

第一类斯特林数（无符号的）

它的组合意义是把个整数拆分成个环排列的个数。

考察数字的位置：

是一个单元素的环，情况数是
在某个圈上，这等同于在拆分成个环排列里，找一个位置插入，情况数是因此

额外补充上定义；以及时。这样在以后的求和式里我们默认不写求和指标的取值范围，让它取遍所有非负整数即可，因为实际上只有其中有限个整数使得对应项不为 0。

用数学归纳法证明：

用代入，知。因此上式添加一个符号项，就得到

再用代替，得到

整理得到将称作有符号的第一类斯特林数，记作，有的资料里也记作。

第二类斯特林数

有的资料里也把它记作或。它的组合意义是把个整数拆分为的非空集合的拆分方式。我们考虑某个特殊元素在拆分中的位置：

独自在一个单元集合中，情况数
在某个集合内，这等于说在个数拆分为个集合时，把放进其中某个集合内，情况数综上

同样可以用数学归纳法证明

证明略。

斯特林数的更多恒等式

由于斯特林数建立了升幂、降幂和普通幂之间的展开关系，而二项式系数本身就可以看作是利用降幂定义的：，因此二项式系数和斯特林数之间存在一些很直观的恒等式。

之前我们看到，有符号的第一类斯特林数把展开成，而第二类斯特林数又可以把转化为。这意味着如果我们连续展开两次，就得到一个恒等变换。用矩阵的语言描述就是矩阵和矩阵互为逆矩阵。

展开写成求和形式就是在说

其中是 Kronecker delta 记号，两个脚标相等时取，否则取。当两个矩阵乘积是单位阵时，它们交换相乘依然是单位阵。所以上式还可以反过来写，得到

Stirling’s Formula

我们证明简化的版本，忽略系数。 Sketch: 取对数，用的积分去估算

注意，这里用到了两个估计：

在此基础上取对数即可

Balls & Bins （球盒模型）

设有个小球，放入个盒子中，问有多少种不同的放置方案？

分别考虑小球，盒子是否相同，分为如下四种情况。

小球不同，盒子不同：Power

每个小球有种选择，共种方案。

小球相同，盒子不同: Number of Solutions of Equation

设第个盒子中放个球，则这个问题的解的集合可以表示为即求方程的非负整数解。令，则有 (隔板法)，该问题等价于在个空中，插入个隔板，结果为。

小球不同，盒子相同：Stirling Number Summation

对球进行编号，上述问题可描述为将小球划分为个集合其中互不相容且无序，求可能的数目。 (集合分拆问题)，把一个有个不同元素的集合分解成个非空集合的不交并，答案就是第二类斯特林数：盒子放球时可能是有空盒子，因此我们可以考虑恰好有个盒子是空盒子的情况，因此剩余的个盒子都是非空的。那么不同的方案数是

小球相同，盒子相同：Partition Number

上述问题可描述为把正整数分拆成至多个数之和，求可能情况数。正整数的一个分拆是把表示成称为“部分”(part)的一个或多个正整数的无序和的一种表示，设表示正整数的不同分拆的数目，简单观察可知，等于下面方程的非负整数解的个数。

恒等式

Vandermonde’s Identity (范得蒙恒等式)

根据二项式定理：拆分幂指数上的求和：组合解释：A 班有人，B 班有人，共挑选人。直接一起挑选，就是 RHS。先从 A 挑选人，再从 B 挑选人，就是 LHS。

Hockey-stick Identity (朱世杰恒等式)

杨辉三角某一个斜边上前个数的和